Bài toán : Cho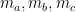 
là ba trung tuyến và 
là ba đường cao của một tam giác có diện tích 
. Chứng minh rằng : ![h_am_a^4+h_bm_b^4+h_cm_c^4\geq 9\sqrt[4]{3}.S^{2}\sqrt{S}](http://s0.wp.com/latex.php?latex=h_am_a%5E4%2Bh_bm_b%5E4%2Bh_cm_c%5E4%5Cgeq+9%5Csqrt%5B4%5D%7B3%7D.S%5E%7B2%7D%5Csqrt%7BS%7D&bg=ffffff&fg=000&s=0 "h_am_a^4+h_bm_b^4+h_cm_c^4\geq 9\sqrt[4]{3}.S^{2}\sqrt{S}")
là ba trung tuyến và là ba đường cao của một tam giác có diện tích . Chứng minh rằng :
Lời giải
Viết lại điều cần chứng minh :
![\dfrac{2S}{a}.\dfrac{(2c^2+2a^2-b^2)^2}{16}+\dfrac{2S}{b}.\dfrac{(2a^2+2b^2-c^2)^2}{16}+\dfrac{2S}{c}.\dfrac{(2b^2+2c^2-a^2)^2}{16}\geq 9\sqrt[4]{3}S^{2}\sqrt{S}\Leftrightarrow \dfrac{(2c^2+2a^2-b^2)^2}{8a}+\dfrac{(2a^2+2b^2-c^2)^2}{8b}+\dfrac{(2b^2+2c^2-a^2)^2}{8c}\geq 9\sqrt[4]{3}S\sqrt{S}](http://s0.wp.com/latex.php?latex=%5Cdfrac%7B2S%7D%7Ba%7D.%5Cdfrac%7B%282c%5E2%2B2a%5E2-b%5E2%29%5E2%7D%7B16%7D%2B%5Cdfrac%7B2S%7D%7Bb%7D.%5Cdfrac%7B%282a%5E2%2B2b%5E2-c%5E2%29%5E2%7D%7B16%7D%2B%5Cdfrac%7B2S%7D%7Bc%7D.%5Cdfrac%7B%282b%5E2%2B2c%5E2-a%5E2%29%5E2%7D%7B16%7D%5Cgeq+9%5Csqrt%5B4%5D%7B3%7DS%5E%7B2%7D%5Csqrt%7BS%7D%5CLeftrightarrow+%5Cdfrac%7B%282c%5E2%2B2a%5E2-b%5E2%29%5E2%7D%7B8a%7D%2B%5Cdfrac%7B%282a%5E2%2B2b%5E2-c%5E2%29%5E2%7D%7B8b%7D%2B%5Cdfrac%7B%282b%5E2%2B2c%5E2-a%5E2%29%5E2%7D%7B8c%7D%5Cgeq+9%5Csqrt%5B4%5D%7B3%7DS%5Csqrt%7BS%7D&bg=ffffff&fg=000&s=0 "\dfrac{2S}{a}.\dfrac{(2c^2+2a^2-b^2)^2}{16}+\dfrac{2S}{b}.\dfrac{(2a^2+2b^2-c^2)^2}{16}+\dfrac{2S}{c}.\dfrac{(2b^2+2c^2-a^2)^2}{16}\geq 9\sqrt[4]{3}S^{2}\sqrt{S}\Leftrightarrow \dfrac{(2c^2+2a^2-b^2)^2}{8a}+\dfrac{(2a^2+2b^2-c^2)^2}{8b}+\dfrac{(2b^2+2c^2-a^2)^2}{8c}\geq 9\sqrt[4]{3}S\sqrt{S}")
Theo BĐT 
:
:![\dfrac{(2c^2+2a^2-b^2)^2}{8a}+\dfrac{(2a^2+2b^2-c^2)^2}{8b}+\dfrac{(2b^2+2c^2-a^2)^2}{8c}\geq \dfrac{[3(a^2+b^2+c^2)]^2}{8(a+b+c)}\geq \dfrac{(a+b+c)^4}{8(a+b+c)}=\dfrac{(a+b+c)^3}{8}=p^3](http://s0.wp.com/latex.php?latex=%5Cdfrac%7B%282c%5E2%2B2a%5E2-b%5E2%29%5E2%7D%7B8a%7D%2B%5Cdfrac%7B%282a%5E2%2B2b%5E2-c%5E2%29%5E2%7D%7B8b%7D%2B%5Cdfrac%7B%282b%5E2%2B2c%5E2-a%5E2%29%5E2%7D%7B8c%7D%5Cgeq+%5Cdfrac%7B%5B3%28a%5E2%2Bb%5E2%2Bc%5E2%29%5D%5E2%7D%7B8%28a%2Bb%2Bc%29%7D%5Cgeq+%5Cdfrac%7B%28a%2Bb%2Bc%29%5E4%7D%7B8%28a%2Bb%2Bc%29%7D%3D%5Cdfrac%7B%28a%2Bb%2Bc%29%5E3%7D%7B8%7D%3Dp%5E3&bg=ffffff&fg=000&s=0 "\dfrac{(2c^2+2a^2-b^2)^2}{8a}+\dfrac{(2a^2+2b^2-c^2)^2}{8b}+\dfrac{(2b^2+2c^2-a^2)^2}{8c}\geq \dfrac{[3(a^2+b^2+c^2)]^2}{8(a+b+c)}\geq \dfrac{(a+b+c)^4}{8(a+b+c)}=\dfrac{(a+b+c)^3}{8}=p^3")
Cần chứng minh : ![p^{3}\geq 9\sqrt[4]{3}S\sqrt{S}\Leftrightarrow p^{6}\geq 81\sqrt{3}S^{3}](http://s0.wp.com/latex.php?latex=p%5E%7B3%7D%5Cgeq+9%5Csqrt%5B4%5D%7B3%7DS%5Csqrt%7BS%7D%5CLeftrightarrow+p%5E%7B6%7D%5Cgeq+81%5Csqrt%7B3%7DS%5E%7B3%7D&bg=ffffff&fg=000&s=0 "p^{3}\geq 9\sqrt[4]{3}S\sqrt{S}\Leftrightarrow p^{6}\geq 81\sqrt{3}S^{3}")
Điều này luôn đúng vì theo 
:
:![S^{3}=\sqrt{[p(p-a)(p-b)(p-c)]^3}\leq \sqrt{\left [ p.\dfrac{(p-a+p-b+p-c)^3}{27} \right ]^{3}}=\sqrt{\dfrac{p^{12}}{27^{3}}}=\dfrac{p^{6}}{\sqrt{27^3}}=\dfrac{p^{6}}{81\sqrt{3}}](http://s0.wp.com/latex.php?latex=S%5E%7B3%7D%3D%5Csqrt%7B%5Bp%28p-a%29%28p-b%29%28p-c%29%5D%5E3%7D%5Cleq+%5Csqrt%7B%5Cleft+%5B+p.%5Cdfrac%7B%28p-a%2Bp-b%2Bp-c%29%5E3%7D%7B27%7D+%5Cright+%5D%5E%7B3%7D%7D%3D%5Csqrt%7B%5Cdfrac%7Bp%5E%7B12%7D%7D%7B27%5E%7B3%7D%7D%7D%3D%5Cdfrac%7Bp%5E%7B6%7D%7D%7B%5Csqrt%7B27%5E3%7D%7D%3D%5Cdfrac%7Bp%5E%7B6%7D%7D%7B81%5Csqrt%7B3%7D%7D&bg=ffffff&fg=000&s=0 "S^{3}=\sqrt{[p(p-a)(p-b)(p-c)]^3}\leq \sqrt{\left [ p.\dfrac{(p-a+p-b+p-c)^3}{27} \right ]^{3}}=\sqrt{\dfrac{p^{12}}{27^{3}}}=\dfrac{p^{6}}{\sqrt{27^3}}=\dfrac{p^{6}}{81\sqrt{3}}")
Ta có điều phải chứng minh.
Không có nhận xét nào:
Đăng nhận xét
Chào các bạn đã ghé thăm blog. Hi vọng các bạn sẽ có được nhiều điều bổ ích từ blog. Các bạn có thắc mắc nào hãy để lại ý kiến tại đây. Tất cả những nhận xét của các bạn vô cùng quan trọng để cho blog phát triển.